покажите как в память компьютера будет записано число 122

Ответы по параграфу 19 Числа в памяти компьютера

Задание 1. Как в памяти компьютера представляются целые положительные и отрицательные числа?

Задание 2. Укажите, каков был бы диапазон значений целых чисел, если бы для их хранения использовалась четырехразрядная ячейка.

Задание 3. Запишите внутреннее представление следующих десятичных чисел, используя восьмиразрядную ячейку: а) 32; б) –32; в) 102; г) –102; д) 126; е) –126.

а) 32 число положительное
32₁₀ = 100000₂
Ответ: 00100000

б) –32 число отрицательное
1) 32₁₀ = 00100000₂
2) Обратный код: 11011111
3) Прибавим единицу: 11011111 + 1 = 11100000
Ответ: 11100000

в) 102 число положительное
102₁₀ = 1100110₂
Ответ: 01100110

г) –102 число отрицательное
1) 102₁₀ = 01100110₂
2) Обратный код: 10011001
3) Прибавим единицу: 10011001 + 1 = 10011010
Ответ: 10011010

д) 126 число положительное
126₁₀ = 1111110₂
Ответ: 01111110

е) –126 число отрицательное
1) 126₁₀ = 01111110₂
2) Обратный код: 10000001
3) Прибавим единицу: 10000001 + 1 = 10000010
Ответ: 10000010

Задание 4. Определите, каким десятичным числам соответствуют следующие двоичные коды восьмиразрядного представления целых чисел: а) 00010101; б) 11111110; в) 00111111; г) 10101010.

а) 00010101 число положительное
10101₂ = 1*2 4 + 1*2 2 + 1 = 16 + 4 + 1 = 21₁₀
Ответ: 21

б) 11111110 число отрицательное
1) Вычтем единицу: 11111110 – 1 = 11111101
2) Обратный код: 00000010
3) 10₂ = 2₁₀
Ответ: –2

в) 00111111 число положительное
111111₂ = 1*2 5 + 1*2 4 + 1*2 3 + 1*2 2 + 1*2 1 + 1 = 32 + 16 + 8 + 4 + 2 + 1 = 61₁₀
Ответ: 61

г) 10101010 число отрицательное
1) Вычтем единицу: 10101010 – 1 = 10101001
2) Обратный код: 01010110
3) 1010110₂ = 1*2 6 + 1*2 4 + 1*2 2 + 2 = 64 + 16 + 4 + 2 = 86₁₀
Ответ: –86

Источник

Представление чисел в компьютере

После того, как мы узнали об основных единицах для измерения информации необходимо разобраться с тем, как в ЭВМ хранятся различные типы данных. В этой статье мы поговорим про представление чисел в компьютере.

Основные понятия и положения

Прежде чем начать разбираться в теме, следует понимать, что все ЭВМ, на данный момент времени, работают с двоичной системой счисления. Это значит, что и вся информация (звуковая, графическая или текстовая) хранится в памяти ПК в виде последовательностей нулей и единиц.

Схематично компьютерная память выглядит так, как показано на схеме ниже:

Как видно из рисунка внутренняя память представляет собой разряды, каждый из которых содержит один бит информации (0 или 1). А восемь битовых кластеров образуют один байт (машинное слово).

Машинное слово – минимально адресуемая ячейка памяти, которую за раз можно обработать командой процессора. То есть минимально процессор может обработать один байт.

Отсюда также вытекает правило, что данные в компьютере представляются дискретно (отдельно). В качестве примера приведем изображение на мониторе. Оно состоит из точек (пикселей). Цвет же каждой точки задается последовательностью из 0 и 1.

Представление чисел в компьютере

Существует несколько вариантов для отображения чисел в ЭВМ, и зависят они от формата числа.

Представление целых чисел в ЭВМ

Для представления целых чисел, в вычислительных машинах существует несколько способов, которые используют 8,16, 24 или 32 разряда памяти (1, 2, 3 и 4 байта).

Первым способом является беззнаковое представление. С его помощью представляются только целые положительные величины, которые не участвуют в арифметических операциях и выступают в роли констант (дата, время и т.д.).

Чтобы представить число в беззнаковой форме необходимо перевести его в двоичную систему счисления и дополнить с начала нулями до нужной разрядности (дополняем до 1,2,3 или 4 байт).

Также следует отметить, что есть ограничения на количество чисел, которые можно представить в n разрядной ячейке. Для беззнаковых величин оно составляет ​\( 2^n \).

Пример: Перевести 54 в беззнаковый формат.

Находим представление 54 в бинарной системе счисления:

\( 1) \ 54:2 \ = \ 27 \ | \ Остаток \ 0 \)
\( 2) \ 27:2 \ = \ 13 \ | \ Остаток \ 1 \)
\( 3) \ 13:2 \ = \ 6 \ | \ Остаток \ 1 \)
\( 4) \ 6:2 \ = \ 3 \ | \ Остаток \ 0 \)
\( 5) \ 3:2 \ = \ 1 \ | \ Остаток \ 1 \)

Итого ​ \( 54_ <10>\) равняется \( 110110_ <2>\). ​​

Дополняем результат до одной из стандартных разрядностей (8 бит) = 00110110.

Ответ: 00110110.

Для представления чисел, которые участвуют в вычислительных операциях, используется представление со знаком. В такой форме записи старший разряд всегда отводится под знак (0 для положительных чисел и 1 для отрицательных).

В случае со знаковым представлением также существуют ограничения. Так как один разряд отводится под знак, то в n-разрядную ячейку можно записать \( (2^ -1) \) положительных и ​\( 2^ \) отрицательных значений.

Также следует отметить следующую особенность — все отрицательные значения в компьютере хранятся в обратном или дополнительном коде, а положительные в прямом.

Для того чтобы перевести число в обратный и дополнительный код вам надо:

Почему же для хранения отрицательных чисел используют обратный или дополнительный код? Это позволяет изменить операцию вычитания на операцию сложения. В противном случае компьютеру бы каждый раз приходилось выяснять, где положительная величина, а где отрицательная и после этого сравнивать их модули, для определения конечного знака, что очень сильно усложняло бы весь алгоритм.

Представление вещественных чисел

Всего существует два способа для представления множества вещественных значений – естественная или экспоненциальная форма.

В жизни мы пользуемся естественной формой. Так число 42,6 мы можем записать несколькими способами. Например:

В компьютере же используется экспоненциальная форма записи. Выглядит она так:

Здесь m – мантисса, которая представляет собой правильную дробь (в правильных дробях числитель меньше знаменателя).

q – система счисления, в которой представлено число.

P – порядок.

В ЭВМ отводится один разряд под знак мантиссы, один под знак порядка и различное число бит под саму мантиссу и порядок. Данный формат записи называется «С плавающей запятой».

Чем больше бит отводится под мантиссу, тем точнее представляемая величина, чем больше ячеек отводится под порядок, тем шире диапазон от наименьшего числа, до наибольшего числа, представляемого в компьютере при заданном формате.

Так как компьютерная память величина дискретная и конечная, то и множество вещественных чисел, с которым работает ЭВМ также конечно.

Видео

Заключение

Вот мы и разобрались с представлением чисел в компьютере и информатике. Краткий материал из данной статьи вы можете использовать для своей онлайн-презентации. При возникновении вопросов оставляйте их в комментариях.

Источник

Урок 28
Числа в памяти компьютера

Основные темы параграфа:

— представление целых чисел;
— размер ячейки и диапазон значений чисел;
— особенности работы компьютера с целыми числами;
— представление вещественных чисел;
— особенности работы компьютера с вещественными числами.

Содержание урока

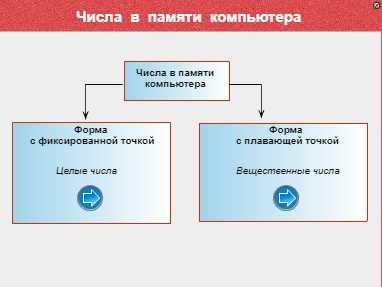
Представление целых чисел

Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры, были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном итоге сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр, — 0 и 1. Поэтому современные компьютерные технологии называют цифровыми технологиями. В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера. Представление целых чисел Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальный размер ячейки, в которой может храниться целое число, — 8 битов, или 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так: Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями. Самый старший разряд — первый слева — хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код: Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 2 7 = 128. Значит: Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127. Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. Но в компьютере все несколько сложнее. Для представления отрицательных целых чисел используется дополнительный код. 1) записать внутреннее представление соответствующего ему положительного числа +Х — это мы уже умеем; 2) записать обратный код полученного числа заменой во всех разрядах 0 на 1 и 1 на 0; 3) к полученному числу прибавить 1. 1) 00011001 2) 11100110 3) +1 В результате выполнении такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения. 0 0 0 1 1 0 0 1 + 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается нолъ. Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом. Следующая страница Размер ячейки и диапазон значений чисел Источник Поделиться с друзьями Вам также может понравиться как подключить яндекс телефон к компьютеру Подключить смартфон к головному устройству Для подключения смартфона к головному устройству автомобиля как переслать папку на другой компьютер Как передать файлы с компьютера на компьютер — 10 способов 2019 года Как передать файлы Чаще всего такая как отправить видео с ноутбука на телевизор по wifi 4 способа подключения ноутбука к телевизору через Wi Fi Синхронизация лэптопа и ТВ с помощью беспроводной как загрузить фото с компьютера на вайбер Как передать фото с компьютера на Viber Viber – это не просто мессенджер, это очень полезное приложение настроить хонор 20 лайт как модем для ноутбука Как включить режим модема на Хонор Смартфоны способны выполнять почти все основные функции компьютера. как восстановить ноутбук делл Восстановление заводских настроек Dell Inspiron В этой статье будет пошаговая инструкция по восстановлению как войти в интернет на ноутбуке через смартфон 3 способа подключить интернет к ноутбуку через телефон Android или IOS Современный мобильный телефон как включить ноутбук асус при черном экране Как легко исправить черный экран ноутбука Asus How Fix Asus Laptop Black Screen Easily Если вы включаете Правообладателям Политика конфиденциальности Наши статьи Контакты