как делать лабиринт на компьютере

Как создать игру “Лабиринт” в PowerPoint

Обучающие игры в виде небольшого путешествия с участием игровых персонажей достаточно часто встречаются в педагогической практике.

Такая интерактивная игра может использоваться:

Для создания таких игр можно воспользоваться обычным офисным приложением PowerPoint. Возможностей этого приложения достаточно для педагога, который не знаком с программированием и просто является пользователем программы для создания презентаций.

Рассмотрим порядок создания игры “Лабиринт”.

Идея игры взята из курса по робототехнике «Робокласс». Игровые персонажи — инфики: ВсеЗнайка, Самоделкин, Кибернетик. Графические объекты — элементы LEGO Mindstorms. Школьнику необходимо преодолеть лабиринт, отвечая на вопросы, которые ему задают инфики. В случае правильного ответа на все вопросы лабиринт будет пройден.

1. Разберем подробно этап создания игры в программе PowerPoint.

А. Формируем лабиринт с помощью каких-либо графических фигур и рисунков. Это может быть множество колес или иные объекты. Добавим фоновое изображение — шестерёнку.

В игре будет предусмотрено три вопроса и три героя, которые будут озвучивать эти вопросы играющему. Для демонстрации вопросов можно использовать изображение электронного табло. Для движения по лабиринту используем изображение робота.

Б. Добавляем текстовое сообщение о том, что для начала игры необходимо кликнуть мышкой по роботу. Для перехода к следующему вопросу игры используем стрелку. Эта стрелка будет появляться только в случае правильного ответа.

Игровое поле готово. Оно понадобится нам для всех трех вопросов. Поэтому можно этот слайд продублировать дважды. По ходу игры будем убирать героев, которые уже задали свои вопросы. А робота будем перемещать по лабиринту.

В. Приступаем к созданию анимационных эффектов для графических изображений и текстового содержимого.

Итак, все слайды готовы. Не забудьте похвалить школьника, успешно прошедшего лабиринт.

2. Публикуем созданную интерактивную игру с помощью программных продуктов iSpring. Теперь эту игру можно разместить в интернете или использовать на занятии в компьютерном классе.

Пример игры доступен здесь.

А если у вас есть идеи для полезных статей на тему электронного обучения — напишите нам в комментариях, и мы будем рады поработать над новым материалом.

Система дистанционного обучения для бизнеса

Поставит на автопилот развитие сотрудников.
Быстрый старт онлайн‑обучения за 1 день.

Источник

Классические алгоритмы генерации лабиринтов. Часть 1: вступление

Предисловие

На написание статьи меня сподвигло практически полное отсутствие материалов на русском языке про алгоритмы генерации лабиринтов. На Хабре, из того, что вообще есть по теме, можно отметить две статьи: раз и два. Ценность и пользу из которых несет лишь вторая. В первой – просто перевод формального алгоритма и небольшое его пояснение. Что, конечно, неплохо, но очень скудно и не вызывает желания изучать тему дальше.

Если моя статья Вам понравится, я продолжу писать о различных алгоритмах. Мы рассмотрим два самых примитивных и простых случая – генерация двоичного дерева и Сайдвиндер, который, по своей сути, просто чуть измененная версия двоичного дерева с одним заметным плюсом. ОСТОРОЖНО ТРАФИК.

Дам один совет – не подглядывайте в код до тех пор, пока вы не напишите свою реализацию. Вы получите гораздо больше удовольствия и пользы от исправления багов и поиска ошибок, чем если просто переведете с одного языка на другой.

Серьезно. Прислушайтесь к совету. Вы, верно, потратите больше времени, но оно стоит стоит. У меня, например, из-за пары ошибок появился очень забавный генератор «инопланетных» текстов, который можно использовать в различных Sci-Fi играх для создания текста. Надеюсь, Вы изучаете тему для себя и никуда не спешите.

Я буду использовать термин «смещение», предполагая английский bias. Т.е. пристрастие алгоритма к направленности в какую-либо сторону. Например, правое смещение – алгоритм генерирует лабиринты с длинными правыми проходами.

Раскраска лабиринтов происходит относительно расстояния от крайнего левого угла поля до некоторой клетки. Чем дальше от начальной координаты – тем темнее будет цвет.

Идеальный лабиринт – такой лабиринт, в котором одна клетка связана с другой одним единственным путем. Иначе говоря, остовное дерево.

Когда я только начинал закапываться в тему лабиринтов, я не предполагал, что в итоге буду писать статью и выбрал язык, на котором у меня есть возможность не тратить слишком много времени на рендер и архитектуру и заниматься исключительно логикой. В итоге, между C++ и Lua, выбор пал на Lua и Love2D.

Не стоит переживать, если Вы с Луа незнакомы. Незнание языка никак не помешает Вам понять реализацию, благодаря простоте синтаксиса. Если Вы хотя бы немного умеете программировать, 80% кода не вызовет у Вас проблем с пониманием. Остальные 20% — language specific, про которые я всегда буду писать вначале статьи, объясняя их работу.

Первое, что мне следует сказать:
Lua имеет лишь одну структуру данных – таблицы – ассоциативный массив, при помощи которого мы создаем нужные нам структуры. К примеру, классы, множества, обычные массивы, стаки, очереди и тому подобное. Обращаться к ним мы может либо с помощью строчных-ключей, либо с помощью индексов.
Так же, таблицы не ограничивают нас в хранении только одного типа данных в одном объекте и работают подобно структурам в C/C++. Такой код абсолютно корректен:

Присваивание nil удалит поле:

Второе:
Lua не имеет скрытого механизма копирования таблиц. Код, приведенный ниже, не будет копировать и создавать нового объекта SomeNewArray, он лишь скопирует в него ссылку на объект SomeArray, и, следовательно, будет изменять его точно так же, как если Вы передадите значение через неконстантную ссылку или указатель в C/C++:

И третье, для тех, кто хорошо знаком с Lua:
Да, я знаю, что в некоторых местах код избыточен. И то, что в некоторых местах всё можно было бы упростить метаметодами тоже. Следует учитывать то, что код писался в первую очередь для того, чтобы разобраться с алгоритмами, а не для использования в реальном проекте. К тому же, отсутствие избытка специфических для языка функций позволяет выкладывать код в том виде, в котором он есть, без нагромождений комментариев.

Алгоритм двоичного дерева

Самый первый и самый простой алгоритм в понимании, который я рассмотрю. Его суть заключается в том, чтобы проложить путь в случайном направлении из каждой клетки поля: в моей реализации либо наверх, либо вправо (зависит от выбранного Вами смещения). Мы обрабатываем только 1 клетку за единицу времени, следовательно, мы можем генерировать лабиринты бесконечного размера, сохраняя лишь конечный результат (лабиринт) без необходимости хранить какую-либо побочную информацию.

Такой способ генерации имеет два побочных эффекта:

1. Лабиринты обладают сильным диагональным смещением и отсутствием тупиков в его направлении. Посмотрите на скриншоты выше и Вы увидите, что каждый из коридоров стремится к правой верхней клетке, и, как итог, имеет ровно один путь к ней, и нигде на пути нет тупика:

2. Два пустых коридора по сторонам лабиринта. Когда алгоритм «прокапывается» до конца строки/столбца, ему не остается выбора, кроме как продолжить путь в одном единственном направлении, создавая пустые «границы».

К слову, название не просто так совпадает со структурой данных. Результат его работы – случайное двоичное дерево, в котором из каждой клетки (вершины) есть ровно 1 путь по направлению к корню (родительской вершине), и, соответственно, ровно 1 путь к любой другой клетке. Как следствие, любая клетка имеет не более 3 соединений со своими соседями.

Формальный алгоритм (для северо-восточного смещения):

Зеленое – текущая рассматриваемая клетка, красное – фронт, клетки, в которые можно переместиться.

Начинаем с координаты (0;0). Наверх в этом ряду пойти не можем, так как иначе выйдем за границы лабиринта. Идем вправо до упора, по пути снося все стены.

Всё, тупик. Идти некуда. Перемещаемся на следующий ряд и видим, что теперь есть возможность пойти наверх и вправо.

Кидаем монетку и выбираем… Верх. Убираем стену и переходим к следующей клетке.

Отлично. Случай подсказывает нам идти направо. Убираем стену и перемещаемся в следующую клетку.

Выбора у нас нет, налево пойти не можем, значит, убираем стену сверху и идем на следующий ряд.

Монета убеждает нас пойти направо. Что же, слушаемся. Убираем стену и переходим к слеудующей клетке.

Прокатившись метр, наш несчастный кусок металла падает и говорит, что пора идти наверх. Сносим стену, шагаем к следующей клетке, и, так как она крайняя в этом ряду, убираем стену сверху. Лабиринт закончен.

Алгоритм «Sidewinder»

Алгоритм с непереводимым названием Sidewinder по своей работе очень похож на алгоритм двоичного дерева, в том отличии, что в нём нет характерного смещения по диагонали, одного пустого коридора и клетки мы рассматриваем не по отдельности, а множествами. Лабиринты получаются с преимущественно вертикальным или горизонтальным смещением (в зависимости от реализации), с отсутствием тупиков в их направлении. В сравнении со своим более примитивным собратом, смещение не так заметно и больше похоже на «спираль», которая плавно сменяет вертикальные и горизонтальные коридоры.

Что касается побочных эффектов, то Sidewinder создает только один пустой коридор на одной стороне, вместо двух. Начиная создание множеств с первого ряда поля, у нас отсутствует возможность прокопать путь наверх, так как мы находимся в самом крайнем вертикальном положении и попытка пойти выше приведет к выходу за границы поля. Но и если мы будем организовывать множества без выхода по вертикали, мы создадим несколько изолированных друг от друга областей.

Для примера: 9 клеток первого ряда можно поделить на три множества, между которыми расположены стены. Каждое множество второго ряда будет прокапывать путь к одному из трех «блоков» выше. Третий ряд проложит путь к «блокам» второго. И так до конца поля. В итоге, у нас получатся 3 разветвленные, изолированные друг от друга вертикальные области, что не подходит для идеального лабиринта, в котором из каждой точки поля есть ровно 1 путь в любую другую.

Формальный алгоритм (для стандартного смещения):

Красные клетки – члены множества.
Мы начинаем с первого ряда и видим, что выше нас – выход за пределы поля. Сносим все стены и идем сразу во второй ряд, создаем пустое множество.

Так, а вот тут интереснее. Давайте добавим в множество первые две клетки ряда.

Выбираем одну из этих клеток и убираем относящуюся к ней верхнюю стенку в первый ряд.

Обнуляем множество, добавляем в нее следующую клетку ряда.

В этот раз ни с кем не объединяем, просто прокладываем путь наверх прямо из этой единственной клетки.

Повторяем наши действия. Обнуляем множество, переходим в следующую клетку, добавляем её… А так как она осталась последней в ряде, то так же убираем стену сверху и идем в ряд ниже.

А теперь сразу объединяем три первые клетки в одно множество.

Случайно выбираем клетку, в нашем случае, вторую и убираем стену сверху к предыдущему ряду.

Ну, тут у нас опять нет выбора, убираем стену наверху и идем на ряд ниже.

На этот раз, самую перваую клетку мы сделаем единственной. Убираем стену к предыдущему ряду и идем дальше, в следующую клетку.

Предположим, что захотели в конце объединить три клетки.

И снова нам приглянулась средняя клетка из множества, из которой и убираем стену наверх. Всё, наш лабиринт готов.

Эпилог

Надеюсь, Вам понравилась статья и Вы почерпнули новые знания о примитивной процедурной генерации лабиринтов. Я выбрал два самых простых в реализации и работе алгоритма, чтобы новичкам было проще «пощупать» тему и понять, хотят ли они изучать её дальше. Мне важно знать, интересны ли такие статьи людям на Хабрахабре и стоит ли продолжать их писать. Для читателей у меня есть еще минимум 9 классических алгоритмов, которые стоит рассмотреть. Какие-то представляют из себя случайное блуждание по полю, как, например, алгоритм Прима или Уилсона, какие-то требуют больше ресурсов для работы, так как работают с графами, например, Эллер и Крускал, а какие-то выдерживают золотую середину. Но и это не конец – у меня в рукаве есть такие вещи, как: полярные (круглые) лабиринты, генерация лабиринтов на различной сетке (гексы, треугольник и пр.), маскинг лабиринтов в надписи и формы, 2.5Д лабиринты и 3Д, теория лабиринтов, статистическое сравнение алгоритмов, комбинированные алгоритмы генерации. В конце концов, у нас есть еще огромное множество вариаций типов лабиринтов. Например, сейчас мы рассматриваем идеальные алгоритмы, в которых из каждой точки есть ровно один путь в любую другую. Но ведь есть еще и те, которые позволяют одной клетке иметь несколько путей для любой другой! Например, Quake, Doom и прочие шутеры в только-только зарождающемся жанре использовали такие алгоритмы для генерации уровней, по некоторым слухам.

Поэтому, если Вам понравилась статья, тема, и Вы хотите видеть их дальше – то, пожалуйста, напишите об этом в комментарии. Так же, буду очень рад любой критике, как в техническом плане, так и в лингвистическом и стилистическом.

Источник

Labyrus: 3D лабиринт

«У тебя 2 минуты, чтобы создать лабиринт, на выход из которого нужна минута.»
Коб, «Начало»

Labyrus — открытая кроссплатформенная многопоточная сетевая игра, написанная с использованием OpenGl и Qt.

Обозначения

Лабиринт состоит из «клеток». Стенки могут стоять только между клетками.
n — ширина лабиринта,
n — длина лабиринта (основание лабиринта — квадрат),
h — высота лабиринта.

Генерация карты

Сначала создается полый кубик. Затем создается список всех возможных стенок внутри этого кубика в случайном порядке. После этого по-очереди пытаемся добавить стенки. После каждого добавления карта проверяется на связность dfs’ом. Итого получается дерево.

Оценка времени работы

количество клеток: n * n * h,
количество стенок: 3 * n * n * h,
время работы dfs’а: n ^ 4 * h ^ 2 (не оптимально храню граф),
время генерации: O(n ^ 6 * h ^ 3).

10 минут, генерится за 0.4 с, что, в принципе, выполняет поставленную задачу. (Оправдание лени)

Лабиринт с h=1. Режим разработчика. Вид сверху.

Описание исполняемых файлов

Управление

Общая схема

Сначала нужно поднять сервер. Затем игроки подключаются к серверу. В момент, когда подключается заданное на сервере количество игроков, начинается игра. Все падают вниз сквозь стены на старт. Изначально вы ориентированы на выход. Он расположен всегда на том же этаже, что и вы — в противоположном углу. При параметре —strong дальнейшие подключения невозможны. Выигрывает игрок, первым дошедший до выхода. После того, как последний игрок доходит до финиша, генерится новая карта, и игра перезапускается.

Источник

Генерация и решение лабиринта с помощью метода поиска в глубину по графу

В этой статье речь пойдет о самом простом в реализации алгоритме генерации «идеального» лабиринта и его применении для поиска пути.

Мы рассмотрим алгоритм, основанный на бэктрекинге, позволяющий создавать лабиринты без циклов, имеющие единственный путь между двумя точками. Алгоритм не самый быстрый, довольно требователен к ресурсам, по сравнению с алгоритмом Эйлера или Крускала, но очень прост в реализации и позволяет создавать ветвистые лабиринты с очень длинными тупиковыми ответвлениями.

Заинтересовавшихся — прошу под кат.

В русскоязычном интернете очень мало информации по алгоритмам генерации лабиринтов, что и стало причиной для написания этой статьи.
Примеры кода на языке Си, а также полный исходный код проекта на GitHub доступны под лицензией GNU GPLv3.
Ссылки на англоязычные ресурсы и проект вы найдете в конце статьи.

Описание алгоритма

Замечание: предполагается, что изначально у каждой клетки есть стенки со всех четырех сторон, которые отделяют ее от соседних клеток.

1. Сделайте начальную клетку текущей и отметьте ее как посещенную.
2. Пока есть непосещенные клетки
1. Если текущая клетка имеет непосещенных «соседей»
1. Протолкните текущую клетку в стек
2. Выберите случайную клетку из соседних
3. Уберите стенку между текущей клеткой и выбранной
4. Сделайте выбранную клетку текущей и отметьте ее как посещенную.
2. Иначе если стек не пуст
1. Выдерните клетку из стека
2. Сделайте ее текущей
3. Иначе
1. Выберите случайную непосещенную клетку, сделайте ее текущей и отметьте как посещенную.

Вы, вероятно, заметили что при выполнении условия 3, готовый лабиринт вероятнее всего будет иметь изолированную область.
Это условие включено в алгоритм в порядке исключения, на практике при нормальной работе алгоритма и правильных исходных данных, оно не выполняется никогда.

Реализация

Как уже сказано выше, предполагается, что при начале работы алгоритма все клетки отделены стенками.

Иллюстрация работы алгоритма

Функция getNeighbours возвращает массив непосещенных соседей клетки

Функция removeWall убирает стенку между двумя клетками:

Сначала вычисляется значение разности координат второй и первой точек. Очевидно, значение может быть либо отрицательное, либо положительное, либо 0.

Надо найти такие координаты xy, чтобы при сложении их с координатами первой точки получались координаты стенки.

Так как мы точно знаем, что вектор разности между координатами стенки и первой точке равен либо (|1|, 0) либо (0, |1|), мы можем этим воспользоваться.

Итак, теперь у нас есть генератор лабиринтов, который может строить запутанные лабиринты, размер которых ограничен только размером оперативной памяти.

В итоге, мы можем получить что-то такое:

Генерация работает, теперь дело за малым: найти в таком лабиринте выход.

Алгоритмов поиска пути несколько больше, чем алгоритмов генерации, и некоторые из них, если будет интерес читателей, я освещу в следующих статьях, но пока что будем довольствоваться тем, что есть, и «пройдем» лабиринт тем же алгоритмом.

И все еще сильнее упрощается, так как нам больше не надо убирать стенки.

Алгоритм поиска пути бэктрекингом:
1. Сделайте начальную клетку текущей и отметьте ее как посещенную.
2. Пока не найден выход
1. Если текущая клетка имеет непосещенных «соседей»
1. Протолкните текущую клетку в стек
2. Выберите случайную клетку из соседних
3. Сделайте выбранную клетку текущей и отметьте ее как посещенную.
2. Иначе если стек не пуст
1. Выдерните клетку из стека
2. Сделайте ее текущей
3. Иначе выхода нет

Выходной точкой, как и стартовой, может выступать любая точка лабиринта, не являющаяся стенкой.
Традиционно, выход должен быть «прижат» к одной из стенок, но по сути может находиться где угодно.
Все таки, в данном случае, «вход» и «выход» — всего лишь две точки, между которыми надо найти путь.

Критерий нахождения «выхода» очень прост: достаточно сравнить координаты текущей точки и координаты «выхода»: если они равны, путь между стартовой и выходной точками найден.

Посмотрим что вышло:

Красным обозначен путь, голубым — посещенные клетки.
100×100

500×500

8000х8000

Вот и все, что нужно для самой простой реализации генератора случайных лабиринтов.

Для тех, кто заинтересовался, полный исходный код проекта на GitHub: Maze Generator and Solver (offscreen rendering)

Источник

Генератор лабиринтов

Рисуем лабиринты любого размера.

Попробуем сделать элегантную алгоритмическую игрушку — лабиринт. Сначала специальный алгоритм будет рисовать для нас случайный лабиринт, а потом мы сделаем так, чтобы его можно было пройти.

Что тут будет интересного:

За основу мы возьмём код Сергея Григоровича и адаптируем его под нашу задачу.

Можно создавать лабиринты любой степени сложности.

Логика проекта

Изначально лабиринт полностью заполнен стенами, в нём нет ходов и свободных мест. Чтобы внутри лабиринта появились маршруты, по которым можно двигаться, мы запустим в лабиринт виртуальный трактор. Он стартует со случайной клетки и расчищает лабиринт до тех пор, пока он не будет готов.

Чтобы понять, готов лабиринт или нет, используем такое свойство лабиринта: если на всех чётных ячейках нет стен, значит, этот лабиринт можно пройти.

👉 Чётные места — это такие места в лабиринте, которые по оси X и Y одновременно имеют чётные координаты. Например, клетка с координатами (2,6) чётная, потому что 2 и 6 чётные числа, а с координатами (2,7) — нет.

Подготовка

Проект пока будет состоять из двух частей:

Дальше мы добавим скрипт, который нарисует наш лабиринт, а потом научим делать всё остальное.

Сейчас сделаем первую часть: напишем HTML-код.

Сейчас это просто пустая страница, на которой ничего не видно кроме заголовка. Когда мы напишем скрипт и добавим его на страницу, то в консоли сможем увидеть черновую версию лабиринта.

Создаём скрипт

За создание будет отвечать отдельный скрипт — назовём его generateMaze.js и сразу добавим его в HTML-файл:

Чтобы скрипт создавал лабиринт нужного нам размера, объявим функцию так:

function generateMaze (columnsNumber, rowsNumber) <>

Всё остальное будем писать внутри этой функции.

Делаем карту и заполняем её стенами

Нам нужно завести отдельную переменную, в которой будет храниться вся карта лабиринта, и на первом этапе заполнить её полностью стенами, чтобы трактору было что чистить:

Готовим трактор к выезду

Чтобы наш трактор работал как нужно, мы должны сделать несколько подготовительных вещей: научиться проверять числа на чётность и выбирать случайные координаты лабиринта на карте.

Проверка на чётность делается просто — объявляем новую функцию и передаём ей число на проверку. Если вернёт true — число чётное.

Со случайными координатами тоже всё легко: берём случайное число в диапазоне от 0 до размера массива, получаем значение ячейки с нужным индексом и возвращаем его:

Ставим трактор в лабиринт

Теперь у нас есть всё что нужно для установки трактора. Единственное сложное место в коде — получение стартовых координат. Для этого мы делаем сложный трюк:

Очищаем клетку с трактором

Чтобы трактор не стоял в стене, нам нужно очистить клетку, на которой оказался трактор. Для этого напишем функцию setField() — она записывает переданное значение по нужным координатам. Смысл её в том, что она сразу проверяет, а правильные ли координаты мы ей передали. Если с координатами всё в порядке, то она сработает; если координат таких в лабиринте нет, то она не будет ничего менять и записывать.

Проверяем, лабиринт готов или нет

Чтобы лабиринт был готов, каждая чётная клетка в нём должна быть пустой. Зная это, напишем простую функцию с проверкой:

Запускаем трактор

Задача трактора — двигаться, очищать и менять направление до тех пор, пока лабиринт не будет готов. Запишем это на языке JavaScript:

Если помните, мы весь этот код пишем внутри большой функции generateMaze(), поэтому, как только лабиринт готов, — мы прерываем её и возвращаем готовую карту. Она нам пригодится на этапе отрисовки.

Выбираем направления и очищаем лабиринт

Последнее, что нам осталось сделать — написать логику движения трактора. Так как он будет постоянно работать с клетками лабиринта, напишем сначала функцию, которая получает значение любой клетки по её координатам. Логика будет такая же, как и в функции setField() — сначала проверяем правильность координат и только потом возвращаем значение.

Логика работы трактора будет такая:

Запишем это в виде кода. Выглядит громоздко, но на самом деле всё просто, комментарии помогут разобраться.

Рисуем лабиринт

Сейчас рисунок лабиринта у нас хранится в массиве.

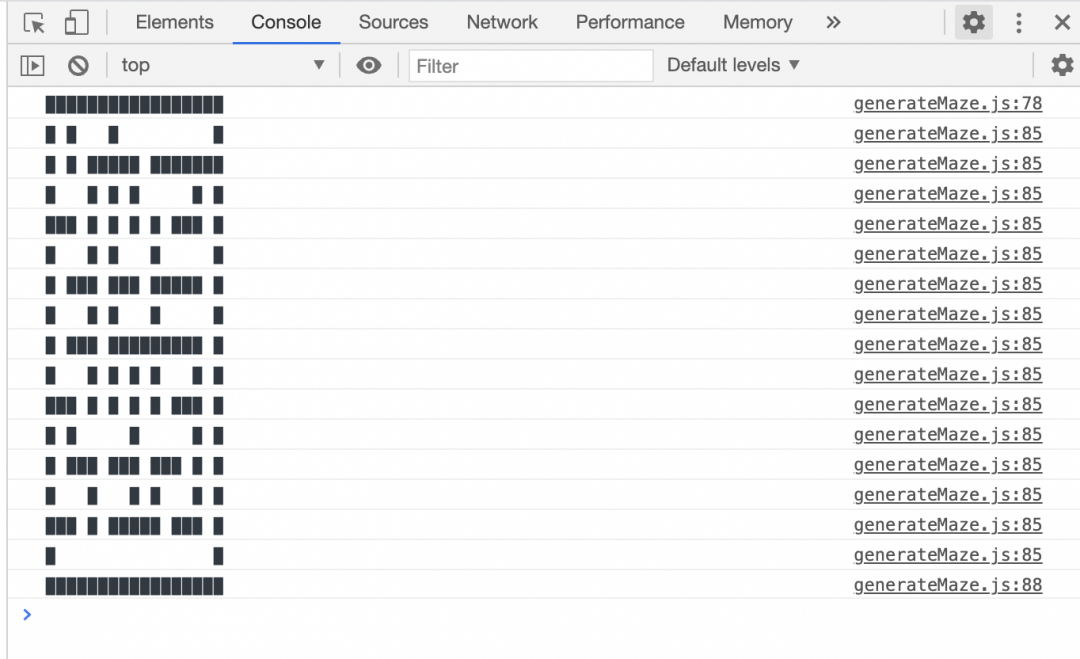
Чтобы нарисовать лабиринт на холсте, нужен отдельный большой скрипт — мы его напишем в другой раз. А пока, чтобы убедиться, что алгоритм работает, мы выведем карту лабиринта в консоли.

У нас уже есть функция, которая проверяет, готов лабиринт или нет. Всё, что нам нужно, — это поместить код вывода на консоль в самый конец этой функции. Вот что у нас получится в итоге:

Запускаем генератор

Для запуска добавляем в HTML-файл скрипт запуска нашей основной функции:

Наш лабиринт в консоли браузера.

Источник